Introduction
Semaphore is a zero-knowledge protocol that allows you to cast a message (for example, a vote or endorsement) as a provable group member without revealing your identity. Additionally, it provides a simple mechanism to prevent double-signaling. Use cases include private voting, whistleblowing, anonymous DAOs and mixers. The original Semaphore circuit was written in Circom. For NRG #3, we implemented Semaphore in Noir with the support of Privacy + Scaling Explorations (PSE) and Aztec Labs. We'd like to thank both teams for sponsoring and their valuable feedback and support during the process.
Summary of achieved work
For this project we rewrote the Semphore circuits in Noir and updated the SDK with respect to the Noir circuit. To make the SDK more suitable for the design of Noir, we also updated the snark-artifacts to load the different Noir circuits and verification keys for different use cases. A big part of Semaphore is the Solidity contracts for on-chain verification. For this, we also updated the design of the contracts to provide seamless transition form the original Semaphore verifier contract to the Semaphore Noir one. Details on the design for the circuit, SDK, and contracts are including in the later part of this report.
One new feature we added to Semaphore that is unlocked by Noir is the batching functionality of proofs. In the original Semaphore, every proof must be verified individually. However, with the recursive proofs feature provided by Noir, we can now batch multiple proofs together and only verify the final result once. This feature also works for the on-chain verifier. That means if we have a large amount of proofs to verify on-chain, we don't have to send one transaction for every proof and pay the transaction fee each time. Instead, we can first batch the proofs together off-chain and only call the on-chain verifier once for the final result. The batching functionality could potentially improve the efficiency for some use cases of Semaphore in the future. More details on this can be found in this part of the report.
We updated the benchmark library for Semaphore so users can run it with the updated circuit. The benchmark result can be found here and here for batching. The current result while being slightly slower than Semaphore in Circom, is very comparable in most settings. Thanks to some of our optimization strategies like pre-computing the verification keys and pre-initializing and reusing the proving backends. Some details of the optimization can be found here.
This report
In this report we first walk through the design of Semaphore in Noir and the benchmarks. Then we focus on the batching function and its benchmarks. Finally we give some future research ideas as well as some potential applications for Semaphore Noir. Along with this report, we also provide two tutorials for Semaphore Noir and the batching functions.
Semaphore in Noir
To learn more about how the Semaphore protocol works we refer to the official docs. In this section we'll share how the Semaphore Noir implementation was done.
Noir circuit
We implemented the Semaphore circuit in Noir. It allows users to prove their group membership without revealing their identities using zero-knowledge proofs.
The witness of the Noir circuit includes the prover's secret key and fields for the Merkle proof. It also takes the scope, a message, the Merkle root, and the nullifier as public inputs. First, the circuit generates the prover's Semaphore identity with the secret key. Then it verifies that the identity is part of the Merkle tree by calculating the Merkle root using the Merkle proof. Afterward, it calculates the nullifier by hashing the scope and prover's secret key. The nullifier can be used to prevent a same proof from being used twice. Finally, the circuit outputs the Merkle tree root and the nullifier that the verifier can check.
Semaphore circuit requires a global value MAX_DEPTH to set the maximum depth of the Merkle tree. The smaller the depth is, the more efficient a circuit will be. However, a Merkle tree can only hold up to $2^{(MAX_DEPTH)}$ members. To allow users to have the best efficiency for every use case, we provide 32 precompiled circuit for MAX_DEPTH from 1 to 32. Users can use the Semaphore SDK to choose the desired precompile as we will explain in the next section.
Below is the flamegraph for the Semaphore Noir circuit for MAX_DEPTH10. This graph indicates how many gates each piece of functionality contributes to the total circuitsize. In this case, acir::blackbox::range accounts for the majority of the gates, due to the fixed setup costs of lookup tables in Barretenberg UltraHonk.

Trusted Setup Considerations
A key advantage of using Noir with UltraHonk compared to Circom with Groth16 is that no trusted setup ceremony is needed for each circuit. In the original Semaphore implementation a separate trusted setup is required for all supported tree depths, since each depth results in a distinct circuit. Because Semaphore supports tree depths 1-32, this results in 32 trusted setup ceremonies. Furthermore, any change to the circuits requires a new trusted setup ceremony.
With Semaphore Noir this overhead is eliminated. The backend used in this project, Barretenberg's UltraHonk, relies on a universal trusted setup and can thus support all tree depths (circuits) without additional ceremonies.
Semaphore SDK
The Semaphore SDK allows users to easily create and interact with a Semaphore group as well as generate and verify proofs. We added several key components such as the proof package, so it now supports Noir proofs.
As mentioned in the last section, to improve efficiency, we precompiled the circuits for MAX_DEPTH from 1 to 32. We also saved the verification keys with respect to each circuit, so users won't have to regenerate the keys every time. The precompiled circuits and verification keys can be found here. The library for downloading and managing circuits and keys can be found here. Users can also provide their own compiled circuits to the SDK instead of using the precompiled one. Note that in order to use the stored verification keys for efficiency, we made some slight modifications to the UltraHonkBackend in the bb.js.
To further reduce proving and verification time, we separate the initialization of a proving backend with the actual proving step. A proving backend is tied to a Noir circuit with a fixed MAX_DEPTH as mentioned above. By doing so, we can reuse the proving backend as long as the MAX_DEPTH of the backend can generate a Merkle tree big enough to hold all the members of the group we are proving or verifying.
Below is the test coverage for the updated Semaphore SDK.
Semaphore Solidity Contracts
We created a new version of the Semaphore Solidity contracts that support Noir proofs. The main contract lets users create and maintain on-chain Semaphore groups. It also allows users to verify zero-knowledge proofs generated by the Semaphore SDK. In order to verify the proofs, we store the 32 verification keys as mentioned above in two contracts (1) (2). As storing all 32 keys in one contract will exceed the contract size limit of 24KB. We also created another key managing contract, and the correct verification key will be loaded based on the Merkle depth value in the proof. The main verifier logic is in SemaphoreNoirVerifier.sol, and it is mostly generated by the Barretenberg proving backend. All necessary contracts were deployed to Sepolia, find the addresses here.
Tutorial
A tutorial of Semaphore Noir can be found here. This tutorial walks you through how to setup and use the packages to create a Semaphore Noir proof and verify it off-chain or on-chain.
Benchmarks for Semaphore Noir
A benchmarking library for Semaphore is provided that will output the benchmarks of the SDK in both node and browser environments. All of those numbers are averages over 10 runs. Additionally, we have benchmarked the gate count directly on the Noir circuit with bb gates.
Machine Details
- Computer: MacBook Air
- Chip: Apple M2 (8-core, 3.49 GHz)
- Memory (RAM): 16 GB
- Operating System: macOS Sequoia version 15.3.1
Version Details
- nargo 1.0.0-beta.3
- bb 0.82.2
- @aztec/bb.js 0.82.2
- @noir-lang/noir_js 1.0.0-beta.3
- @noir-lang/noir_wasm 1.0.0-beta.3
Node Benchmarks
Below we benchmark generating and verifying Semaphore proofs with N-member groups, using circuits with MAX_DEPTH set to K (see Noir circuit) in Node environment. Find and rerun the different benchmarking scripts here.
The benchmarks are split based on whether the proving backend is pre-initialized or not. In all cases we let the prover backend run on the highest possible number of threads (with os.cpus().length) for best performance. There are also benchmarks for the time it costs to initialize the backend.
In practice an application could start loading the proving backend right away; this does not have to happen at the moment of actually creating the proof. Furthermore, this initialization only has to happen once and then proof generation (or verification) can continuously use that backend.
Benchmarks with backend pre-initialized
Generate proofs with proving backend already initialized. (see Semaphore SDK)
| Function | Avg Time (ms) |
|---|---|
| Generate Proof 1 Member [Max tree depth 1] | 296.87 |
| Generate Proof 100 Members [Max tree depth 7] | 412.60 |
| Generate Proof 500 Members [Max tree depth 9] | 454.38 |
| Generate Proof 1000 Members [Max tree depth 10] | 483.66 |
| Generate Proof 2000 Members [Max tree depth 11] | 538.07 |
Verify proofs with proving backend already initialized. (see Semaphore SDK)
| Function | Avg Time (ms) |
|---|---|
| Verify Proof 1 Member [Max tree depth 1] | 14.85 |
| Verify Proof 100 Members [Max tree depth 7] | 15.12 |
| Verify Proof 500 Members [Max tree depth 9] | 15.10 |
| Verify Proof 1000 Members [Max tree depth 10] | 15.06 |
| Verify Proof 2000 Members [Max tree depth 11] | 15.47 |
Benchmarks without pre-initializing the proving backend
Generate proofs (includes backend initialization).
| Function | Avg Time (ms) |
|---|---|
| Generate Proof 1 Member + Initialize backend [Max tree depth 1] | 547.23 |
| Generate Proof 100 Members + Initialize backend [Max tree depth 7] | 705.19 |
| Generate Proof 500 Members + Initialize backend [Max tree depth 9] | 760.26 |
| Generate Proof 1000 Members + Initialize backend [Max tree depth 10] | 822.15 |
| Generate Proof 2000 Members + Initialize backend [Max tree depth 11] | 885.36 |
Verify proofs (includes backend initialization).
| Function | Avg Time (ms) |
|---|---|
| Verify Proof 1 Member + Initialize backend [Max tree depth 1] | 194.27 |
| Verify Proof 100 Members + Initialize backend [Max tree depth 7] | 224.15 |
| Verify Proof 500 Members + Initialize backend [Max tree depth 9] | 233.42 |
| Verify Proof 1000 Members + Initialize backend [Max tree depth 10] | 237.17 |
| Verify Proof 2000 Members + Initialize backend [Max tree depth 11] | 247.10 |
UltraHonkBackend Initialization
The time to initialize proving backends with different circuits.
| Function | Avg Time (ms) |
|---|---|
| Initialize Backend Tree Depth 1 | 185.58 |
| Initialize Backend Tree Depth 10 | 222.44 |
| Initialize Backend Tree Depth 20 | 276.05 |
| Initialize Backend Tree Depth 32 | 365.78 |
Node benchmarks of the Original Semaphore V4
To compare with the original Semaphore implementation using Circom, we include the benchmarks below, all run on the same machine. Both proof generation and verification are around 1.4-1.7x slower for Semaphore Noir, if we assume that the proving backend for Noir will be pre-initialized. Proof generation with Noir ranges from 296-538ms, while the Circom implementation benches between 175-387ms for the different tree depths. Proof verification is 14-15ms versus 8ms.
Proof generation
| Function | Avg Time (ms) |
|---|---|
| Generate Proof 1 Member | 175.45 |
| Generate Proof 100 Members | 284.79 |
| Generate Proof 500 Members | 313.28 |
| Generate Proof 1000 Members | 319.75 |
| Generate Proof 2000 Members | 387.23 |
Proof verification
| Function | Avg Time (ms) |
|---|---|
| Verify Proof 1 Member | 8.58 |
| Verify Proof 100 Members | 8.59 |
| Verify Proof 500 Members | 8.62 |
| Verify Proof 1000 Members | 8.64 |
| Verify Proof 2000 Members | 8.61 |
Browser Benchmarks
The browser benchmarks are ran with pre-initialized proving backend. The script can be checked here.
Proof generation with Noir in browser environment takes about 1-2secs, while Semaphore in Circom only takes about 200~300ms. This is likely caused by the memory limit of the browser, since UltraHonk uses more memory than Groth16 which is used in Circom. It is a future research to optimize Semaphore Noir as well as UltraHonk in the browser environment.
Proof generation
| Function | Avg Time (ms) |
|---|---|
| Generate Proof 1 Member [Max tree depth 1] | 797.18 |
| Generate Proof 100 Members [Max tree depth 7] | 1315.42 |
| Generate Proof 500 Members [Max tree depth 9] | 1457.08 |
| Generate Proof 1000 Members [Max tree depth 10] | 1528.59 |
| Generate Proof 2000 Members [Max tree depth 11] | 1815.77 |
Comparison with original Semaphore
| Function | Avg Time (ms) |
|---|---|
| Generate Proof 1 Member | 167.91 |
| Generate Proof 100 Members | 276.99 |
| Generate Proof 500 Members | 305.99 |
| Generate Proof 1000 Members | 317.27 |
| Generate Proof 2000 Members | 397.70 |
Gas estimates
Estimations of gas usage in the SemaphoreNoir contract.
| Function | Gas Usage |
|---|---|
| SemaphoreNoir.verifyProof 1 Member [Max tree depth 1] | 1856690 |
| SemaphoreNoir.verifyProof 100 Members [Max tree depth 7] | 1887944 |
| SemaphoreNoir.verifyProof 500 Members [Max tree depth 9] | 1887800 |
| SemaphoreNoir.verifyProof 1000 Members [Max tree depth 10] | 1887896 |
| SemaphoreNoir.verifyProof 2000 Members [Max tree depth 11] | 1919115 |
| Function | Gas Usage |
|---|---|
| SemaphoreNoir.validateProof 1 Member [Max tree depth 1] | 1996899 |
| SemaphoreNoir.validateProof 100 Members [Max tree depth 7] | 2027997 |
| SemaphoreNoir.validateProof 500 Members [Max tree depth 9] | 2028057 |
| SemaphoreNoir.validateProof 1000 Members [Max tree depth 10] | 2028093 |
| SemaphoreNoir.validateProof 2000 Members [Max tree depth 11] | 2059288 |
Comparison with Semaphore.sol
In the Semaphore.sol contract for V4 of Semaphore, calling validateProof for 10 members has an estimated gas cost of 285622, and this number is 285598 for 30 members (benchmark reference). Although the above benchmarks don't show exactly those group sizes, we can estimate that validation in SemaphoreNoir.sol is approximately 7x more expensive. In the next section we'll discuss how batching for Noir can be applied to significantly lower the gas cost if the Semaphore proofs get validated in batches rather than individually.
Circuit Gate Counts
Gate counts of the Semaphore Noir circuit of different MAX_DEPTHs.
| MAX_DEPTH | acir_opcodes | circuit_size |
|---|---|---|
| 1 | 2822 | 7756 |
| 2 | 3149 | 8696 |
| 3 | 3476 | 9636 |
| 4 | 3803 | 10576 |
| 5 | 4130 | 11516 |
| 6 | 4457 | 12456 |
| 7 | 4784 | 13397 |
| 8 | 5111 | 14336 |
| 9 | 5438 | 15276 |
| 10 | 5765 | 16217 |
| 11 | 6092 | 17157 |
| 12 | 6419 | 18096 |
| 13 | 6746 | 19037 |
| 14 | 7073 | 19977 |
| 15 | 7400 | 20917 |
| 16 | 7727 | 21857 |
| 17 | 8054 | 22797 |
| 18 | 8381 | 23737 |
| 19 | 8708 | 24678 |
| 20 | 9035 | 25617 |
| 21 | 9362 | 26557 |
| 22 | 9689 | 27498 |
| 23 | 10016 | 28438 |
| 24 | 10343 | 29377 |
| 25 | 10670 | 30318 |
| 26 | 10997 | 31258 |
| 27 | 11324 | 32198 |
| 28 | 11651 | 33138 |
| 29 | 11978 | 34078 |
| 30 | 12305 | 35018 |
| 31 | 12632 | 35959 |
| 32 | 12959 | 36898 |
ZK artifact sizes
In the SDK to generate and verify a Semaphore or Semaphore Noir proof compiled versions of the respective circuits (Circom or Noir) are used. These are called "ZK artifacts" in the Semaphore protocol. In this section we'll compare the sizes of these artifacts for both Circom and Noir.
The Noir ZK artifacts can be found here. Find the Semaphore (Circom) artifacts hosted here (select Project Semaphore and Version 4.0.0).
Proof generation
For proof generation in the Semaphore Circom implementation, a wasm and zkey file are needed. In the case of Semaphore Noir this requires a .json file, which is used to instantiate the proving backend and then passed on to the proving functionality. This is where the Noir artifacts are retrieved.
The table below compares selected depths. The Noir artifact is between 5x and 11x smaller than Circom’s combined .wasm and .zkey files. The smaller the tree, the bigger the difference in artifact sizes.
| Tree Depth | Noir .json | Circom .wasm | Circom .zkey |
|---|---|---|---|
| 1 | 259 KB | 1.71 MB | 1.13 MB |
| 2 | 301 KB | 1.71 MB | 1.24 MB |
| 3 | 342 KB | 1.71 MB | 1.48 MB |
| 4 | 384 KB | 1.71 MB | 1.6 MB |
| 5 | 426 KB | 1.71 MB | 1.71 MB |
| 10 | 635 KB | 1.72 MB | 2.28 MB |
| 15 | 844 KB | 1.75 MB | 3.11 MB |
| 20 | 1.03 MB | 1.75 MB | 3.69 MB |
| 30 | 1.44 MB | 1.76 MB | 5.34 MB |
| 32 | 1.52 MB | 1.77 MB | 5.57 MB |
Proof verification
To verify a proof, a circuit-specific verification key is needed (thus there is a distinct key for each tree depth). For Semaphore Noir, these keys are each around 1.78 KB and for the Semaphore Circom implementation 3.66 KB. So the Noir verification key in comparison is about half the size, for all tree depths.
For Circom all the verification keys together can be found here, and the separate files in the registry mentioned above. For Semaphore Noir, check the verification keys here.
Batching Noir Semaphore proofs
In an effort to lower on-chain verification costs, we added an additional feature for Semaphore in Noir: batching of Semaphore Noir proofs. We achieved this by using recursive proofs in Noir. In this section we'll briefly explain how it works and how to use it.
Batching the Semaphore proofs
To achieve batching we use Noir circuits that verify 2 previously generated proofs, by using the verify_proof functionality:
#![allow(unused)] fn main() { use dep::std::verify_proof; verify_proof( verification_key, proof, public_inputs, key_hash, ); }
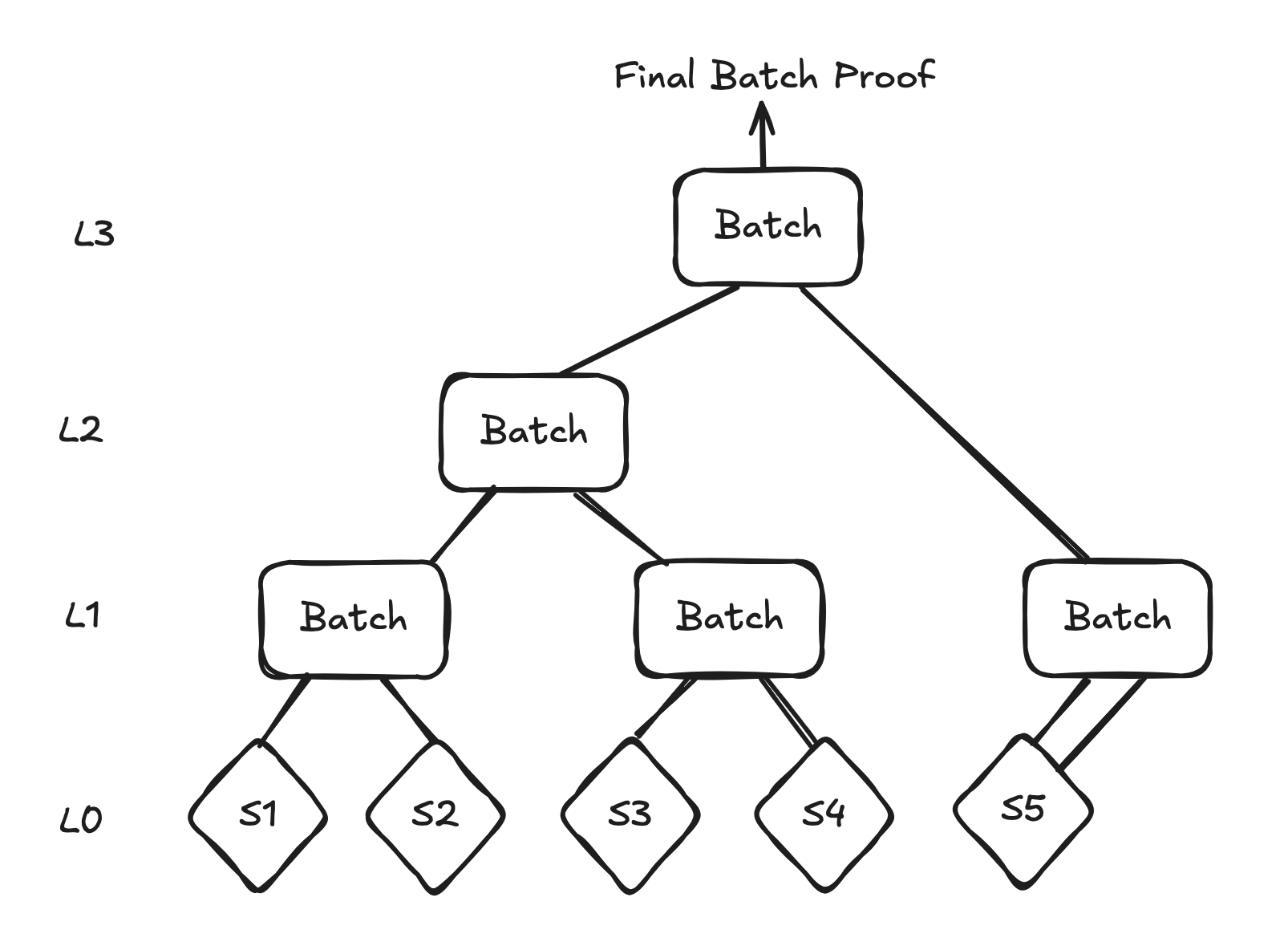
From each pair of Semaphore proofs, we generate a single "Batch proof", which then can be used to be paired up again with other Batch proofs. Doing this repeatedly leads us to a final "root" Batch proof. To account for the fact that our number of Semaphore proofs and intermediate nodes might not form a perfect binary tree with this strategy we handle this as follows:
- If there are an odd number of Semaphore proofs, duplicate the last Semaphore proof
- In the next layers if there is a node without sibling, promote it to the next level. This is how it works in LeanIMT as well, which is the optimized binary tree structure used in Semaphore.
For example, with 5 Semaphore proofs it would work as depicted in the image below: Semaphore proof 5 gets duplicated for self-pairing, and the third Batch proof on L1 gets promoted to L2 for pairing.
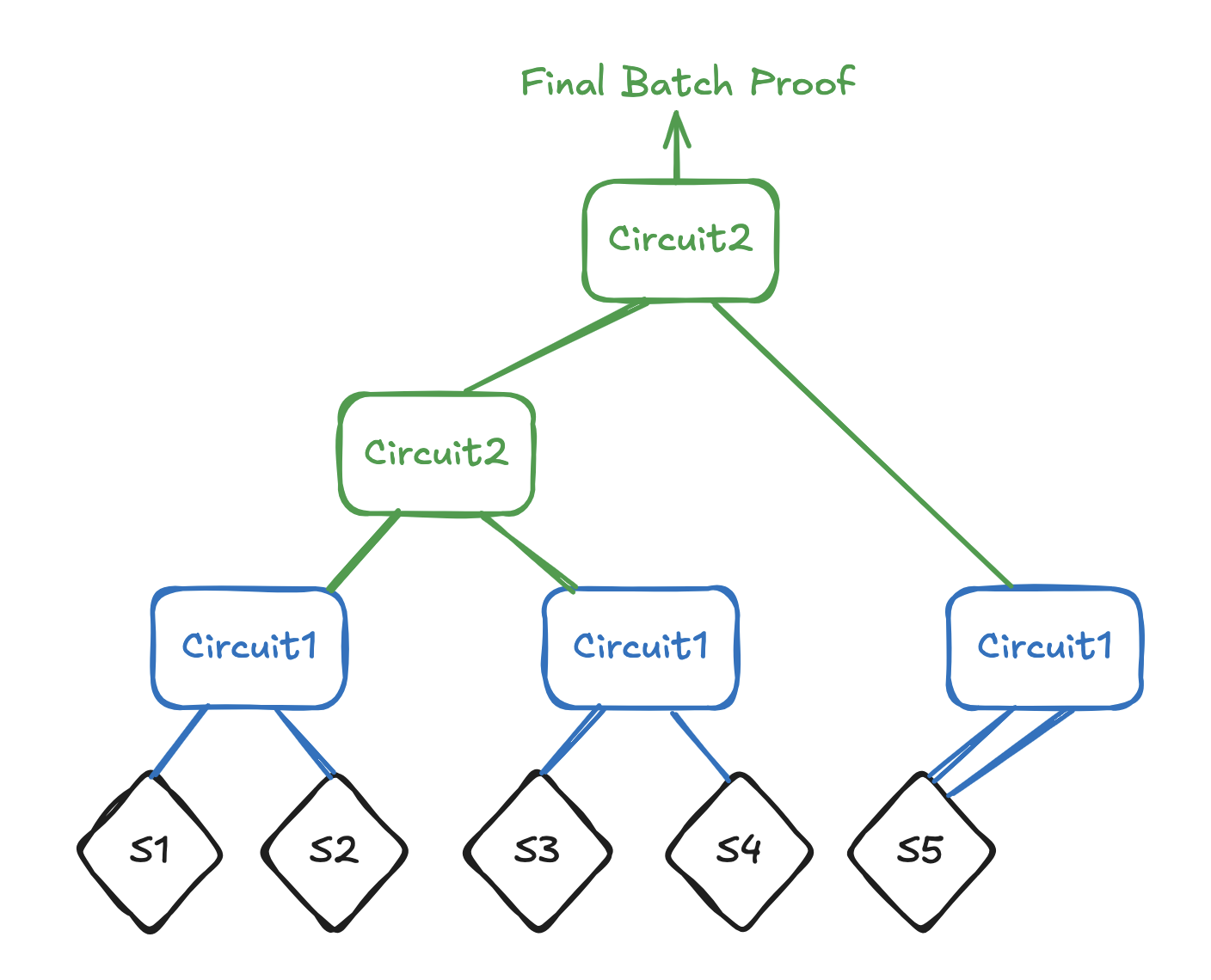
But there is a catch; we can't use the same Batch circuit for all the layers. This is because of the difference in number of public inputs; a Semaphore proof has 4 public inputs, while a Batch proof has 0. This is why we created 2 slightly different batching circuits:
This also explains why a Semaphore proof aren't promoted to the next level if there are an odd number of leaves; it doesn't directly fit the input type for Circuit2. As a solution we chose to self-pair the last leaf, so we start batching after layer 1 with a homogeneous proof type. (Of course, another approach could be to create an additional Batch circuit that takes a Semaphore proof and a Batch proof, but we opted for the least amount of circuits for now.) This full strategy is shown below.
A detail of the implementation is that the final Batch proof can be generated with the keccak flag, which makes it ready for on-chain verification.
Propagation of nullifiers and merkle roots
In the standard "single" Semaphore Noir setting the validateProof function in the smart contract checks a couple of things:
- The zero knowledge proof that was sent is valid
- The nullifier hasn't been used before
- The merkle root used in the proofs is valid (it's either the current merkle root of the group or a previous one)
Lifting this to the batch setting, we still need to take care of the nullifiers and merkle roots that belong to the initial Semaphore proofs. If we only do proof verification in a recursive circuit, there is no public input or output, which means the final batch proof has no public inputs. The validity of the batch proof itself could be verified, but in the context of Semaphore this won't guarantee the validity of the nullifiers and merkle proofs used in the batch.
This problem can be solved by propagating these values up the tree that we use for batching (as explained above). In this way, the initial input values will still be tied to the final batch proof. Then, it can be checked in the smart contract that the nullifiers and merkle roots are valid and that those were indeed the values used in the batched Semaphore proofs.
In practice, we propagate a hash of all the original public inputs for each pair of Semaphore proofs, and apply consequent hashing in the next layers of the batching tree. Specifically it works like this (psuedocode snippets):
- Leaf layer:
#![allow(unused)] fn main() { hash( sem_proof1.scope, sem_proof2.scope, sem_proof1.message, sem_proof2.message, sem_proof1.merkle_root, sem_proof2.merkle_root, sem_proof1.nullifier, sem_proof2.nullifier ) }
- Node layers:
#![allow(unused)] fn main() { hash( batch_proof1.inputs_hash, batch_proof2.inputs_hash ) }
Now, the final batch proof outputs the final hash. This hash is recomputed in the smart contract and used to verify the batch proof. Note that we use keccak for hashing, because this will be cheaper in the smart contract.
Usage details & tutorial
To implement batching we use bb CLI; at the moment it's not possible to use bb.js because the amount of recursion we use leads to memory errors. The upside of this is that bb CLI is faster than using bb.js, the downside is that batching can only be supported by node and not for browsers.
Furthermore, the Semaphore proofs that are used for batching must be generated with a special flag. This can be done with the special function generateNoirProofForBatching.
A full tutorial on how to use batching in a project can be found here.
Benchmarks Batching Noir proofs
In the benchmarking library you can find the functionality to rerun these benchmarks for batching.
The average values below are over 3 runs and always generate the final proof with the keccak flag, so it is ready for on-chain verification. The most important benchmarks here are batch proof generation and the gas cost estimates for on-chain verification, because the main aim for batching is to lower the total gas cost.
Batch Proof Generation
Generation of a batch proof of N Semaphore proofs using the function batchSemaphoreNoirProofs with keccak enabled for on-chain use.
| Function | Avg time (ms) | Avg time (min) |
|---|---|---|
| Generate batch of 10 | 97064 | 1.62 |
| Generate batch of 20 | 214852 | 3.58 |
| Generate batch of 30 | 349871 | 5.83 |
| Generate batch of 100 | 1187020 | 19.78 |
Semaphore proof generation for batching
Since batching uses recursion, we need to generate the Semaphore proof in a different way. For this we have added generateNoirProofForBatching which generates a proof using the bb CLI, see the benchmarks below (benchmark script reference). This form of Semaphore proof generation is slightly faster than the benchmarks we shared above, because bb CLI is faster than bb.js.
| Function | Avg Time (ms) |
|---|---|
| Generate Proof (for batching) 1 Member [Max tree depth 1] | 238.81 |
| Generate Proof (for batching) 100 Members [Max tree depth 7] | 307.53 |
| Generate Proof (for batching) 500 Members [Max tree depth 9] | 336.82 |
| Generate Proof (for batching) 1000 Members [Max tree depth 10] | 350.36 |
| Generate Proof (for batching) 2000 Members [Max tree depth 11] | 389.08 |
Gas estimates on-chain verification on a Batch proof
In the SemaphoreNoir smart contract, a batch proof can be validated with validateBatchedProof. This will verify the batch proof, check that there are no duplicated nullifiers and that all the used merkle roots are correct.
For a single Semaphore Noir proof for a 100 member group, calling validateProof costs an estimate of 2027997 in gas. If we validate a batch of Semaphore Noir proofs, the gas usage is as follows for groups of 100 members:
| Function | Gas Usage | Comparison |
|---|---|---|
| SemaphoreNoir.validateBatchedProof 10 proofs | 2689415 | 1.33x |
| SemaphoreNoir.validateBatchedProof 20 proofs | 3095601 | 1.53x |
| SemaphoreNoir.validateBatchedProof 30 proofs | 3572773 | 1.76x |
| SemaphoreNoir.validateBatchedProof 50 proofs | 4745292 | 2.34x |
| SemaphoreNoir.validateBatchedProof 100 proofs | 8933459 | 4.41x |
As the table shows, batching significantly reduces the per-proof gas cost. For example, 100 proofs can be verified on-chain for only 4.4 times the gas cost of verifying a single proof. As shown earlier, generating such a batch could take around 20 minutes, showing that there's a clear tradeoff between computation effort and time off-chain and gas saved on-chain.
Batch Proof Verification (SDK)
On the application side, it is possible we'd like to verify the batch proof locally before verifying on-chain. This is slightly more costly than verifying a "normal" Semaphore proof with the SDK. Benchmarks for verifyBatchProof:
| Function | Avg time (ms) |
|---|---|
| Verify batch of 10 | 46 |
| Verify batch of 20 | 32 |
| Verify batch of 30 | 31 |
| Verify batch of 100 | 37 |
Outlook
Wrapping up this project, we'd like to share some insights and ideas for future research or other implementation work as well as discuss a bit about what this current project unlocks.
Unlocked applications
The Semaphore Noir application with batching can make a big difference for on-chain voting gas costs in comparison to using the existing Semaphore protocol. Any application that aims to use Semaphore with on-chain verification could prefer the tradeoff that batching offers by spending some extra time on batching the proofs, but having a much lower verification cost. The cost to verify a Noir batch proof will outweigh the cost of verifying separate Circom Semaphore proofs after batching more than ~10 proofs. This means it will mainly be attractive to use for applications that work with a large number of proofs.
Semaphore Proof of non-membership with Noir
In the research notes for Semaphore version 4, there is a feature idea for proof of non-membership. This would allow people who are not part of a certain group to send signals. However, this is not easy to implement with the current structure for groups. We think that with Noir, and specifically recursion in Noir, proof of non-membership could be implemented for Semaphore V4 for small groups.
The members of a group in Semaphore are the leaves of a binary tree (more specifically, a LeanIMT). Each leaf is a hash of the public key of the member. To show you are not part of the group you can show that the hash of your public key is not equal to any of the leaves. If we wrap this in Noir proofs for each leaf and batch them together similarly to how we did it in this project, we think this could be practical for small groups < 100 members.
How could we implement this? For each leaf L_i of the leanIMT, generate a proof that L_i is part of the group and that my leaf x is not equal to it. We can call these our NotLeafProofs.
Then, we can create a batching circuit that takes 2 NotLeafProofs, verifies both proofs and outputs their respective leaves L_i. Finally we have another batching circuit that verifies previous proofs and propagates the hash of the leaves L_i. If we follow the same strategy as the LeanIMT, promoting a single node to the next level, and thus promoting the hash of the leaves to the next level, the resulting hash should be equal to the merkle root of the group.
The end result would be a final Batch proof which can be verified with the merkle root. This merkle root should be equal to the most recent merkle root known in the smart contract (otherwise the leaf could be a newer member). The cool thing is that of course we can also batch these proofs together and ultimately proving multiple non-membership proofs on-chain at once.
Feature suggestions for Noir & bb.js
The first feature request was already mentioned in our progress report: it would be great if a Noir circuit can be parameterized. In the case of Semaphore in Noir there are practically speaking 32 variations of the same circuit, with the difference being a constant which indicated the maximum depth of the merkle tree: pub global MAX_DEPTH: u32 = 10;. Currently, we overwrite this value in a script in order to obtain the circuit we want. It would be great if circuit parameterization would be added to a feature version of Noir! This feature request was already made in GitHub, follow status here.
In addition, in Semaphore Noir we are using an adapted version of the UltraHonkBackend, see code reference here. To increase performance we allow users to reuse verification keys, which required a small adjustment to this class. It is imaginable more developers would like to make use of this option, so maybe this could be added in a future bb.js version. We added this issue in GitHub here.
Parallelizing batching of Semaphore proofs
The current benchmarks for batching of Semaphore proofs does not take into account parallelization. Especially for the first layer of generating the initial Batch proofs, this could make for a significant performance improvement. In general, for batching large number of Semaphore proofs it would be interesting to see how much of an improvement parallelization could mean.
Add Semaphore Noir template to Remix IDE
The Semaphore Circom template was added to Remix IDE a few years ago. More recently, also Noir support was added to Remix! We'd like to leave this observation here in case it is possible and desirable to add the Semaphore Noir template to Remix.
Links
- Semaphore Noir
- snark-artifacts fork and hosting of the Noir artifacts
- Semaphore Noir benchmarking repo
- Tutorial: How to use Semaphore Noir
- Tutorial: Use batching for Semaphore Noir proof
- NRG#3 announcement and our proposal
- Semaphore Noir Project progress report
- Follow HashCloak on X(Twitter)